Uriel Veranos

Problema de la cobertura de vértices

En ciencias de la computación, el Problema de la cobertura de vértices es un problema NP-completo, que pertenece a los 21 problemas NP-completos de Karp. Es muy utilizado en teoría de complejidad computacional para probar la pertenencia a la clase NP-hard de otros problemas computacionales difíciles.

El Problema de cobertura de vértices es un problema de optimización que consiste en encontrar una cobertura de vértices de tamaño k en un grafo dado.

ENTRADA: Grafo G.

SALIDA: El menor número k tal que exista una cobertura de vértices S para G de tamaño k.

Vertex Cover:

Dado un G = (V, A) no dirigido, el problema es encontrar un conjunto de tamaño mínimo C perteneciente a V, tal que C cubra todos los arcos A. Para este problema se plantea un algoritmo heurístico, que no siempre da la mejor solución, pero en general es óptimo.

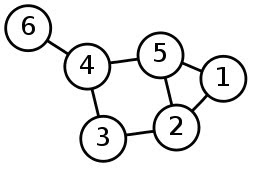
Ejemplo:

En el grafo {1,3,5,6} existe una cobertura de vértices de tamaño 4. Sin embargo, esta no es la cobertura mínima, porque existen las coberturas de vértices {2,4,5} y {1,2,4}, ambas de tamaño 3.

Pseudocodigo del vertex cover (ejemplo):

void eliminar_arcos_incidentes(list &l, int vertice){

list::iterator it = l.begin();

list::iterator borrar;

while(it != l.end()){

borrar = it;

it++;

if (((*borrar)->origen == vertice) || ((*borrar)->destino == vertice))

l.erase(borrar);

}

}

void vertex_cover(grafo g, list & C){

list l;

crear_lista_de_aristas(g,l);

list::iterator it = l.begin();

while(!l.empty()){

//elijo un vertice arbitrario (tomo el 1º)

C.push_front((*it)->origen);

eliminar_arcos_incidentes(l,(*it)->origen);

it = l.begin();

}

}//se podria mejorar ordenando l de mayor a menor por cantidad de incidencia.

***Algoritmo de

aproximacion para el Vertex Cover***

Aproximacion

Un algoritmo cuya respuesta C

está “próxima” a la solución óptima C* se denomina un algoritmo de aproximación. La “proximidad” se mide normalm

ente con el radio ρ(n) que produce el algoritmo cumpliendo que si n es el tamaño de la entrada, max{C/C*,C*/C}≤ρ(n).

Redes

Imagina que tienes una red de componentes. Todos los elementos de la red necesitan de un recurso, por lo que necesitas suministrar dicho recurso a un subconjunto de componentes que cubra todo. Obviamente, te gustaría conectar el mínimo número

de elementos.

Entrada: un grafo no dirigido G=(V,E).

Problema: encontar un conjunto C⊆V de tamaño mínimo tal que por cada (u,v)∈E, o bien u∈C obien v∈C.

Ejemplo:

Observación: Sea G=(V,E) un grafo no dirigido. El complementario Ic de un vertex-cover I es un independent-set de G.

Prueba: Dos nodos de un VERTEX-COVERc no pueden estar conectados por una arista.

----Algoritmo de aproximación para VERTEX-COVER

C := φ

E’ := E

Mientras E’ ≠φ

– Sea (u,v) una arista cualquiera de E

– C:= C ∪ {u,v}

– Eliminar de E’ cualquier arista que tenga u o v como extremo.

-devolver C.

----Tiempo polinómico (O(n2))

• C := φ

•E’ := E ====> o(n2)

• Mientras E’ ≠φ

– Sea (u,v) una arista cualquiera de E’

–C := C ∪ {u,v}

– Eliminar de E’ cualquier arista que

tenga u o v como extremo.

•devolver C.

Nota: El conjunto que construye el algoritmo es un VERTEX-COVER, puesto que se itera hasta cubrir todas las aristas